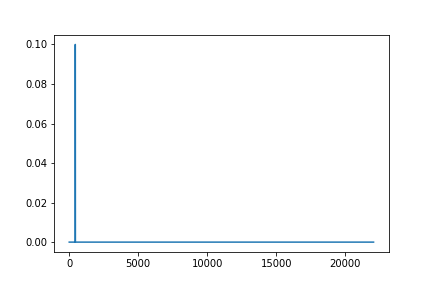
〇正弦波のラ(440Hz)の周波数スペクトル
import numpy as np
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * np.sin(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
plt.plot(F_a[:int(fs/2)+1])
plt.show()
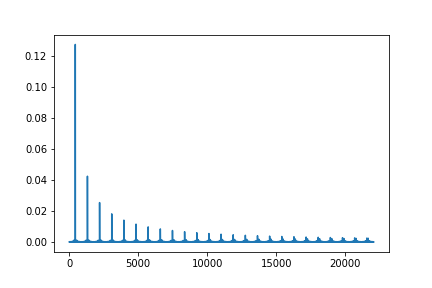
〇矩形波のラ(440Hz)の周波数スペクトル
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.square(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
plt.plot(F_a[:int(fs/2)+1])
plt.show()
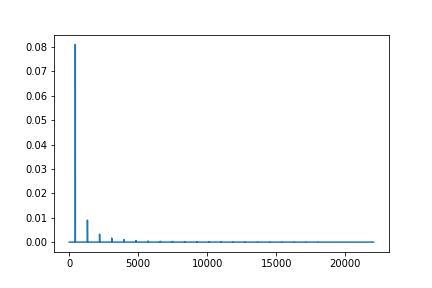
〇三形波のラ(440Hz)の周波数スペクトル
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs + np.pi/2, 0.5)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
plt.plot(F_a[:int(fs/2)+1])
plt.show()
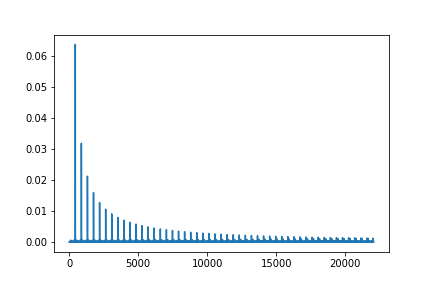
〇のこぎり波のラ(440Hz)の周波数スペクトル
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
plt.plot(F_a[:int(fs/2)+1])
plt.show()
☆Tips
周波数スペクトルから元の波形を再現することができる。
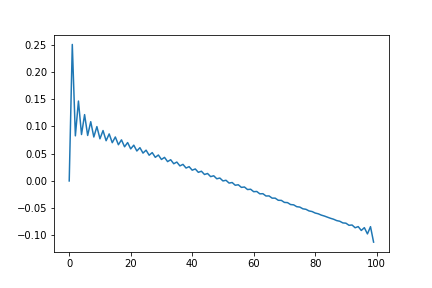
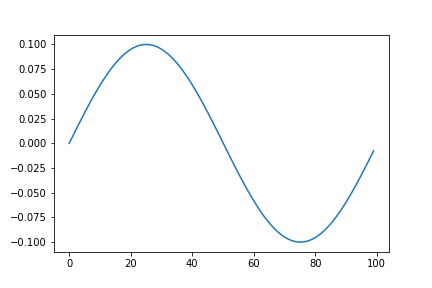
〇正弦波のラ(440Hz)の波形
import numpy as np
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * np.sin(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
F_s = np.zeros(fs)
for i in range(int(fs/2)+1):
F_s += F_a[i] * np.sin(2.0 * np.pi * i * n / fs)
for i in range(fs):
F_s[i] += F_a[0]
plt.plot(F_s[:int(fs/f0)])
plt.show()
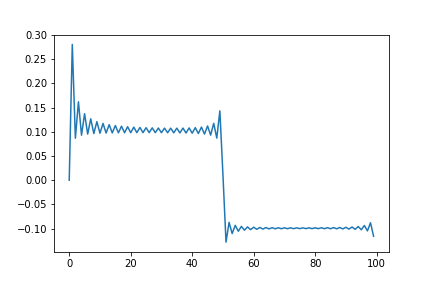
〇矩形波のラ(440Hz)の波形
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.square(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
F_s = np.zeros(fs)
for i in range(int(fs/2)+1):
F_s += F_a[i] * np.sin(2.0 * np.pi * i * n / fs)
for i in range(fs):
F_s[i] += F_a[0]
plt.plot(F_s[:int(fs/f0)])
plt.show()
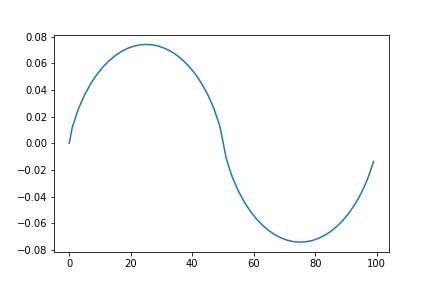
〇三形波のラ(440Hz)の波形
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs + np.pi/2, 0.5)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
F_s = np.zeros(fs)
for i in range(int(fs/2)+1):
F_s += F_a[i] * np.sin(2.0 * np.pi * i * n / fs)
for i in range(fs):
F_s[i] += F_a[0]
plt.plot(F_s[:int(fs/f0)])
plt.show()
〇のこぎり波のラ(440Hz)の波形
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)[0:fs]
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs)
F = np.fft.fft(s)
F_abs = np.abs(F)
F_a = F_abs / fs * 2
F_a[0] = F_abs[0] / fs
F_s = np.zeros(fs)
for i in range(int(fs/2)+1):
F_s += F_a[i] * np.sin(2.0 * np.pi * i * n / fs)
for i in range(fs):
F_s[i] += F_a[0]
plt.plot(F_s[:int(fs/f0)])
plt.show()